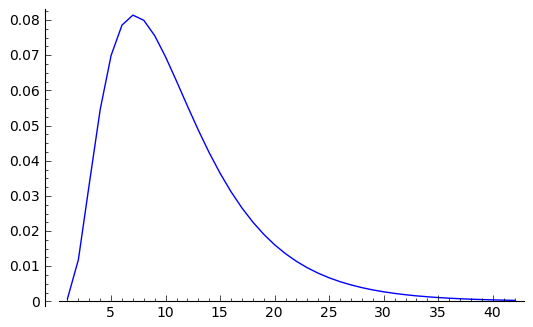
Espérance du nombre de lancers pour faire un yams

J’avais répondu à la question : quelle est la proba de faire un yams quand on garde toujours les dés dont la valeur apparait de façon majoritaire ?

Cette réponse avait entrainé une autre question, dans les commentaires : combien de fois faut-il relancer en moyenne pour obtenir un yams si on garde toujours les dés dont la valeur apparait de façon majoritaire et qu’on n’est pas limité par 3 lancers ?

Avant de vous expliquer mon calcul, je vous donne directement le résultat sous forme d’un graphe (cliquer dessus pour obtenir la version PDF) :

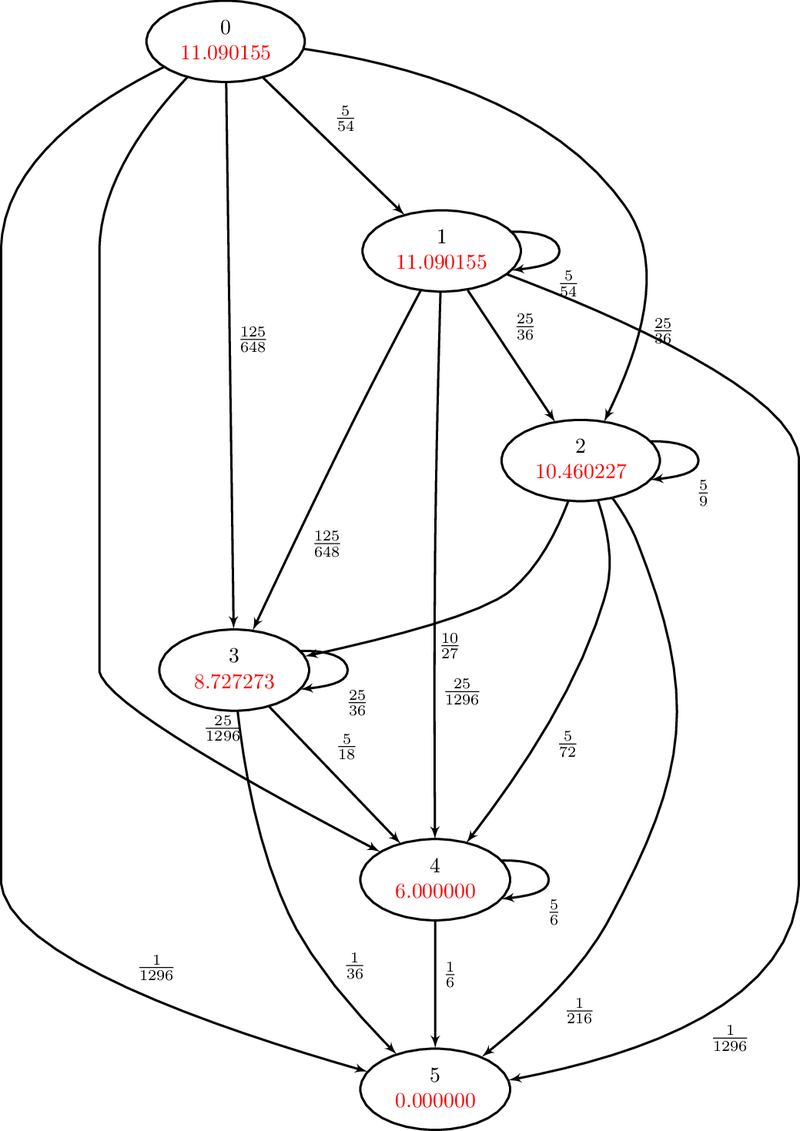
La réponse est donc environ 11 lancers en moyenne pour parvenir à un yams (les nombres en rouge donnent l’espérance du nombre de lancer à effectuer pour parvenir à un yams à partir d’un état donné, par exemple il faudra lancer un peu moins de 9 fois en moyenne lorsqu’on a déjà un brelan).

En fait, je ne calcule pas simplement l’espérance du nombre de lancers pour chaque état, mais la distribution de probabilité complète, par exemple avec mon script SAGE je peux répondre à la question : quelle est la proba que je doive faire exactement 5 lancers pour parvenir à un yams lorsque j’ai déjà une paire ?

Si on essaie de faire les choses naïvement, on se rend compte que si on finit avec exactement 5 lancers à partir d’une paire, c’est que :

1. soit on fait un lancer, passe au brelan, puis il nous faut encore 4 lancers ;
2. soit on reste sur la paire après le premier lancer, et il nous faut encore 4 lancers ;
3. soit on passe sur le carré, puis il faut encore 4 lancers depuis cet état.

Donc si on appelle p(x, y) la proba de finir en y lancers depuis l’état x, on a des dépendances sympathiques entre toutes ces valeurs. Pour m’en sortir, j’associe à chaque état une série formelle dont le coefficient de degré i est égal à la proba d’obtenir un yams en i lancers exactement à partir de cet état. On constate alors que :

1. le graphe de transitions se traduit en des relations simples entre les séries formelles associées à chaque état ;
2. la série formelle A5 associée à l’état 5 est simplement A5 = 1 (on a la certitude de terminer en 0 lancer).
3. chaque série formelle sera en fait une fraction rationnelle ;
4. l’espérance du nombre de lancers pour parvenir à un yams se calcule comme A'(1) si A est la série formelle associée à l’état considéré.

Une fois qu’on a calculé A0(X), il n’y a plus qu’à en faire le développement de Taylor en 0 à l’ordre voulu pour en déduire la proba de finir, du début, en 1 lancer, 2 lancers, etc. Le résultat est reproduit sur le dernier graphe (on constate que le maximum est atteint pour 7 lancers).