Proba de faire un yams

Depuis quelques temps je joue au yams sur un site de jeu de yams en ligne et je me suis naturellement posé des questions sur la probabilité de succès pour certaines figures. Concernant le yams (5 dés identiques), j'adopte la stratégie qui consiste, avant chaque jet, à conserver les dés dont la valeur apparait le plus grand nombre de fois. Après quelques calculs griffonnés sur un coin de table, je me suis dit qu'avec 5 dés qui ne peuvent prendre que 6 valeurs distinctes, l'analyse pouvait aussi bien se faire brutalement par un petit programme. Quelques lignes de SAGE plus tard, je vous propose le graphe suivant (cliquer pour une version en PDF) :

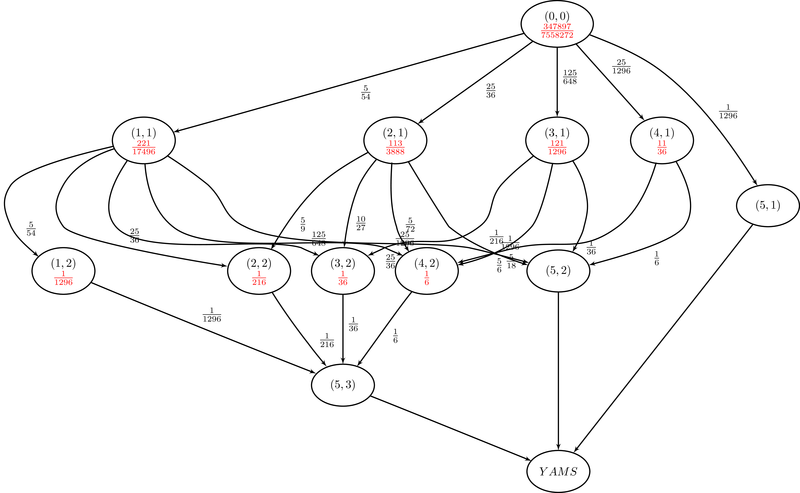
Les transitions sont étiquetées par leur probabilité d'apparition, les nœuds sont étiquetés par la paire (nombre de dés identiques obtenus, nombre de jets effectués), et en rouge est indiquée la proba de succès, c'est-à-dire d'arriver à un yams. Quelques remarques :

• la probabilité d'obtenir un yams avec cette stratégie est d'environ 4,6%, soit environ tous les 22 tours.
• si on s'acharne sur chacun de ses 13 tours (ou 14 avec un joker) à obtenir le yams, au détriment de toute autre figure, on augmente ses chances à un peu plus de 45% (48% avec joker).
• si après le premiet jet on dispose d'un brelan, on a environ 9% de chance de réussite.
• il est absolument ridicule que python ne possède pas un type rationnel, seule raison pour laquelle j'ai utilisé SAGE.

Le script SAGE permet de tester une stratégie qui parait bien raisonnable : lorsque le mieux qu'on puisse garder est un singleton, on relance le tout. On vérifie que cette stratégie ne modifie pas la probabilité de succès.

Le graphe est produit par dot2tex.